统计学中的假设检验

简介 #

药厂宣传新药疗效很好，研究宣称研发的算法比之前的要好或者某项运动是有助于长寿的，我们怎么样来判断这些结果是否靠谱？这些问题就可以用统计学中的假设检验来判断。

统计推断是根据抽样分布规律和概率理论，由样本结果去推论总体特征。它主要包括假设检验和参数估计两个内容。

假设检验的理论依据是“小概率事件原理”。“小概率事件原理”就是概率很小的事件在一次试验中认为是不可能发生的。如果预先的假设使得小概率事件发生了，类似于数学中传统推理的反证法出现逻辑矛盾那样，就认为出现了不合理现象，从而拒绝假设。一般把概率不超过0.10、0.05、0.01的事件当作“小概率事件”，称为检验水准或显著水平，通常取0.05、0.01，实际问题中也可取0.10、0.001等。¹

假设检验步骤 #

提出假设原假设和备择假设 #

• 根据要比较的统计量类型，选择不同的假设检验类型，比如样本均值与指定值，汽车百公里油耗为xx；样本比例，支持率低于30%；样本方差，矿泉水容量的离散程度
• 原假设通常是不存在差异或者没有关联，比如A组和B组均值没有差异；备选假设可以选择左右或双侧（大、小或不等于）
  • 原假设是唯一的，而备择假设有很多，这也是为什么对无差异进行检验的原因，即假设无差异为真来检验到底是不是无差异

抽样（optional） #

• 一般问题就说了自己样本是什么。对于需要实验验证的问题，采样时由于不可能涵盖所有的样本，需要选择合适具有代表性的样本，进行两组比较或者与指定总体样本比较

选择检验统计量 #

• 对假设进行检验的统计量，一般为抽样的样本在原假设情况下符合什么分布，计算对所关注差异或者效果的度量。

统计显著性水平、拒绝域/临界点 #

• 显著性水平：原假设为真时拒绝原假设的概率，一般是0.05。后续计算以原假设为真统计量出现的概率，假如小于显著性水平，即认为出现的概率很低（小概率事件），拒绝原假设。假如原假设确实为真，这里就犯了第一类错误，但是这个概率是我们可以直接设置的。
  • 第一类错误²：没差异判断有差异$\alpha$
  • 第二类错误：有差异判断没差异$\beta$
  • 统计检验能力：有差异能判断出差异，$1-\beta$ 通常需要大雨0.8（Jacob Cohen）
  • 第一类错误和第二类错误的关系
    • 如下图应该选择备择假设，而选了null假设的概率为$\beta$, 可以看到$\alpha$越小，$\beta$越大,无法设置让第一类错误和第二类错误同时变小

    • 

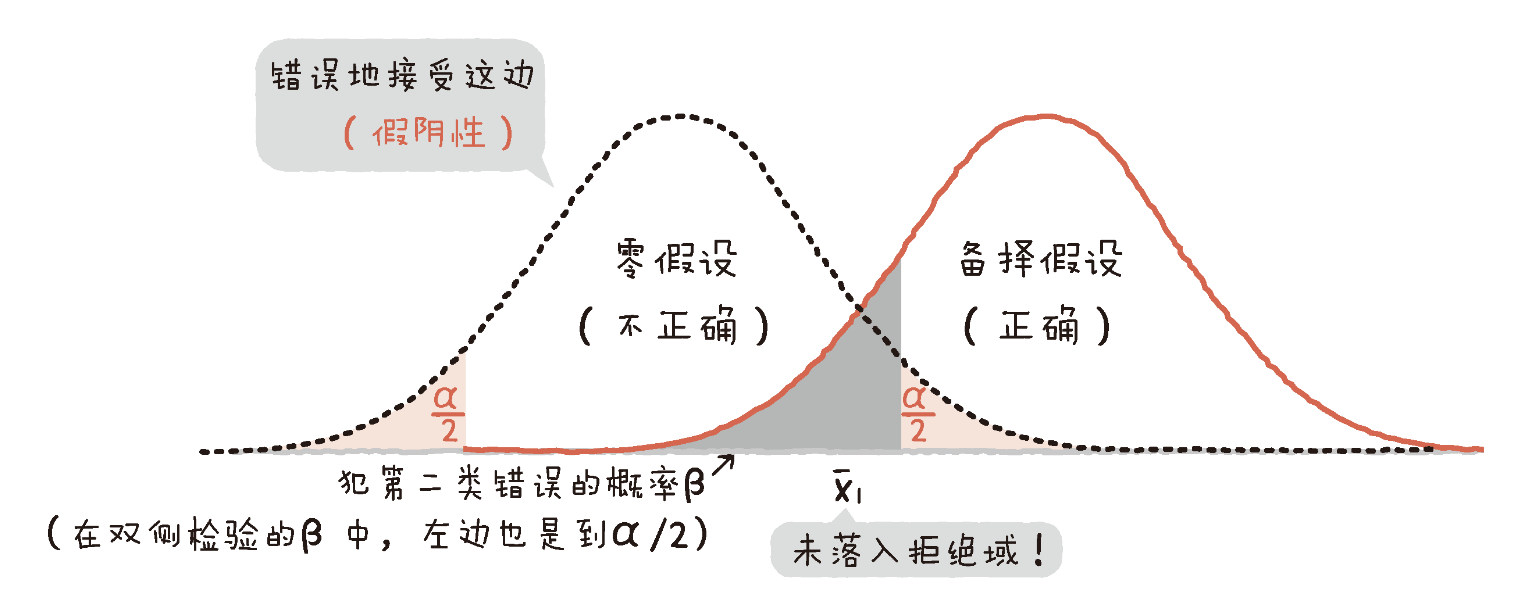
• 拒绝域：根据分布以及显著性水平可以确定拒绝域值

求出检查统计量的p值 #

• 双边或单边某中分布下检验量统计量出现的概率

查看样本结果是否位于拒绝域 #

• 一般通过p与显著性水平比较

决定是否接受原假设 #

• 如果p小于显著性水平，拒绝原假设

案例一 女士品茶 #

以女士品茶为例，一位女士宣称自己可以分辨先奶后茶还是先茶后奶，大家都觉得不可思议，准备了10杯奶茶让其分辨，正确分辨了每一杯，现在问题是是不是真的能分辨？

• 提出原假设和备择假设
  • 原假设：不能分辨
• 选择检验统计量
  • 在不能分辨的情况10次都对，对该事件的度量
• 显著性水平
  • 0.05
• 检验统计量概率：不能分辨就是瞎猜每次判断的概率为1/2 ，该次事件的概率为$(\frac{1}{2})^{10}$
• 判断是否位于拒绝域
  • 远小于显著性水平，落在拒绝域，小概率事件不可能发生，但是在这次实验中发生，说明原假设不对
• 拒绝原假设
  • 即该女士有分辨奶茶先后的能力

案例二 均值检验 #

测定土地PH值是否为7，进行了17次采样，采样结果mean = 6.676， sd= 0.455³

• 提出原假设与备择假设
  • ph为7
• 选择检验统计量
  • 大样本数据一般认为符合正态分布，正态分布的均值$$z=\frac{\bar{x}-\mu_{0}}{\sigma/\sqrt{n}}$$而总体标准差一般很难获取，这时一般用样本标准差来代替，样本统计量服从t分布，上述公式变为$$z=\frac{\bar{x}-\mu_{0}}{s/\sqrt{n}}$$样本的均值应满足上式
• 显著性水平
  • 0.05
• 检验统计量概率
  • 代入公式得t统计量为-2.9，查分布表找到概率为0.009
• 拒绝